圆方树：元芳你怎么看

 

圆方树推荐

 

 

圆方树是什么？

Tarjan家族中，最不好处理的是点双

因为一个割点可能属于很多的DCC。

为了把图缩成一棵树，我们不得不做出这样的处理：

摘自：https://blog.csdn.net/qq_39670434/article/details/81973923

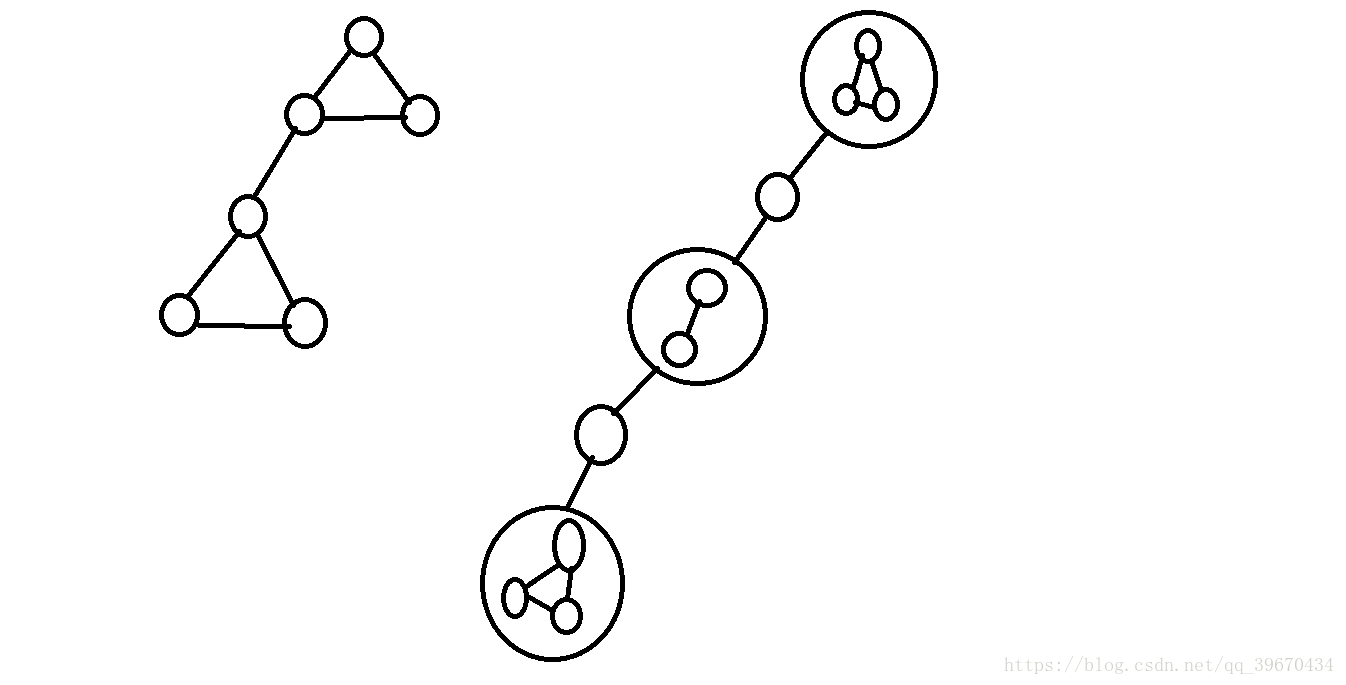
这个树不但丑。而且，对于一个点双内部的信息，我们把它缩成了一个点，内部的与非割点有关的路径我们一无所知。

所以这个玩意只能用来维护连通性。。。。以及简单的问题。

而且要分类讨论一大堆。，。。。

（upda：2019.6.21这个树就是圆方树的虚树，圆方树主要就是多了主干之外的一些圆点作为枝叶。这些枝叶和方点之间的连边可以赋予权值，使得）

 

圆方树横空出世。

摘自yyb博客

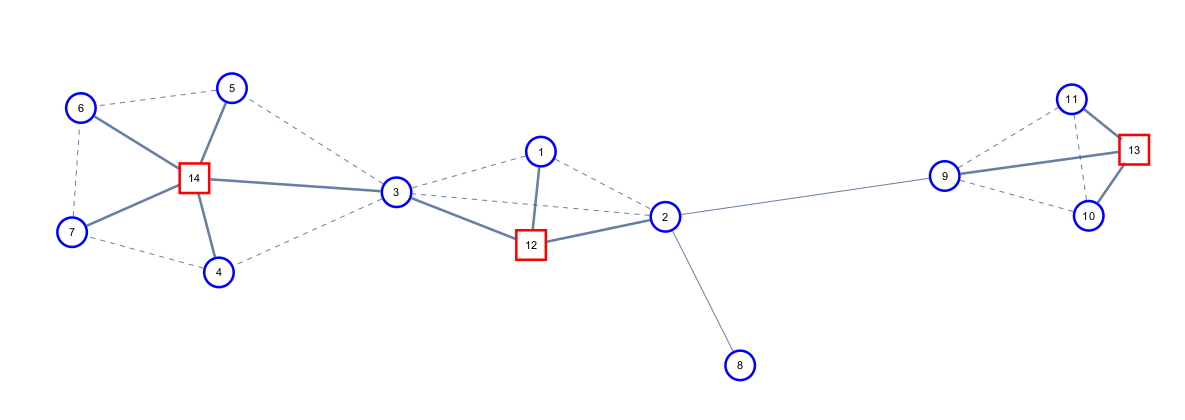
这样，我们

既保留了整体上树的优美结构，又可以保留所有的原始节点。

利用圆点和方点之间的边来存储信息，就可以比较轻松处理具体点双内部的路径了。

 

圆方树是处理仙人掌问题的。

处理仙人掌问题还有一个方法：dfs树。

我们发现一个仙人掌无非就是多了几个环。

那么找一个dfs树出来，就是多了几个返祖边。

dp的时候照顾一下就好了。

例如把环直接拉出来，或者多加一维记录环顶的信息 。

 

但是这个东西的低级之处在于，

基本上我们只能搜索一次，对于重复灵活查询，例如最短路径的问题，就无能为力了。恶心之处就是环的问题。

（可能用什么暴力高级数据结构维护也许可以）

 

圆方树就简单很多了。

一般就分方点原点讨论一下。

关键在于怎么处理圆——方边，以及方点维护哪些信息。

 

由于圆方树比较优秀，

它还可以用于一般的图。

 

 

总之：

既保留了整体上树的优美结构，又可以保留所有的原始节点。

利用圆点和方点之间的边来存储信息，就可以比较轻松处理具体点双内部的路径了。

 

---

 

upda：2019.2.15

博主没有放例题。。。

圆方树既然是树，就和其他树一样了。

仙人掌只是特殊的情况。

关键是方点的权值设计

Tourists——圆方树

结合树链剖分

[APIO2018] Duathlon 铁人两项

结合树形DP

Codeforces某题·改

• 给出一个图，多次询问

• 每次给出一个点集和一个边集

• 询问如果往图中加入了边集里的边，那么点集的点是否点双连通

?, ?, ?, Σ ≤ 10^6

直观感觉：

点双就是一堆莲藕2333

建立圆方树

边连接的两个方点路径上的所有圆点会变成一个DCC

不必暴力缩点，只用考虑关键点

每次询问涉及到的所有的点：点集点，边集连接的点，建立圆方树上的虚树

由于点双没有传递性，所以并查集乱搞都是错的

考虑重新tarjan

那么为了体现之前点双的性质，对于在虚树上的方点，对周围一圈在虚树上的圆点，相邻圆点之间额外连边（加入这次的边集里）像一个方点为轴的车轮

总之要然这些点一定能成为点双

然后加上边集里的边大力跑tarjan，如果点集里的点最终在同一个DCC里，就可以

至于原图可能不连通，找虚树可能困难，可以考虑连超级源

 

Codechef Push the Flow!

对于环上跑最大流怎么整？

一定是分两路，每路都是最小值。

我们把环上最小的边断开，加到环上其他边的容量上

而且仙人掌->树

这样两点间最大流就是两点间的边权最小值！

LCT维护

改变边权的时候要和原来的最小边权讨论一下谁更小